参考书籍:
- 模拟电子技术 第2版:电子工业出版社 (美)Robert L.Boylestad,(美)Louis Nashelsky著
- 模拟电子技术基础(第四版)
- 新概念模拟电路 杨建国著
半导体二极管
半导体基本知识
本征半导体
纯净的,具有晶体结构的半导体成为本征半导体。
本征载流子
仅由于外部原因引起材料中的自由电子称为本征载流子
掺杂半导体
半导体材料可以通过在相对纯净的半导体材料中添加特定的杂质原子来改变其特性,即使只添加千万分之一的杂质。
N型半导体(电子型半导体)
N型半导体是向硅(锗)晶体内掺入五价元素杂质(P/Sb)而形成的。
以磷原子为例,其有五个价电子,与硅原子形成四个共价键后还会多出一个电子,这个剩余的电子与其所属原子间的联系相对松散,只需要外界给予较少的能量就能成为自由电子从而在新构成的N型材料内自由运动。
由于磷原子与硅原子在形成4个共价键后还能给出一个电子,故称磷原子为施主原子,磷成为施主杂质或N型杂质,其中N的意义为Negative。
明显自由电子为多数载流子,空穴为少数载流子。
P型半导体(空穴型半导体)
也是向硅晶体内掺杂,但是掺入三价元素(B/Ga)。
以镓原子为例,其与硅原子形成三个共价键,但是硅原子还剩余一个未成键的自由电子,因此在晶体中形成了空穴,当其相邻共价键上的电子吸收外来能量激发时,就有可能填补上这个空穴,从而在外加电场的作用下形成空穴电流。
由于镓原子和硅原子形成三个共价键后,硅原子并没有形成8电子稳定构型,而是形成了空穴,需要从杂质原子的空位中吸收电子,故称镓原子为受主原子。
明显空穴为多数载流子,自由电子为少数载流子。
PN结
偏置电压
偏置是指为得到一定的响应而在设备两端所加的电压,对于二极管而言,偏置电压的正负与其极性相同。
无偏置
在无外加电场的情况下,当N型半导体和P型半导体结合在一起时,由于两种材料的载流子分布数量恰好相反,因此空穴与自由电子会向对方的区域扩散并结合,使得原来P区和N区的电中性被破坏,在交界面附近形成了一个很薄的空间电荷区,或者说形成了一个内部电场(并非由外加电压形成的),也叫内联电场。虽然这些离子也带电,但是由于物质结构的原因,它们并不能自由移动,因此他们不导电,因此空间电荷区的电阻率很高
在这个区域内,由于多数载流子已经扩散到对方的区域并复合掉,因此此区域也成为耗尽层,其实也就形成了一个二极管
对于内联电场,P区内电子被夺走显正电性,N区内空穴被中和显负电性,明显它对多数载流子的扩散有阻止作用,阻止作用是两方面的,对于N区域来说,首先要克服耗尽层正离子层的引力,其次还要克服负离子层的阻力,才能够到达P区,因此,此时耗尽层也可看为是一个阻挡层,但是其对少数载流子有加强作用,少数载流子会向对方所在的区域漂移,与扩散作用的运动方向恰好相反。并且参与扩散的多子数目等于参与漂移的少子的数目,从而达到动态平衡,空间电荷区不再发生变化,于是形成了稳定的PN结,对于P区与N区杂质浓度相同时,正负离子区的宽度也相同,称为对称结,
当两侧杂质浓度不同时,浓度高一侧的离子区宽度低于浓度低的离子区宽度,此时称为不对称PN结;但是两种结的外部特性都是相同的,即在半导体二极管两端不施加偏置电压时,在单一方向上的电流为零
反向偏置
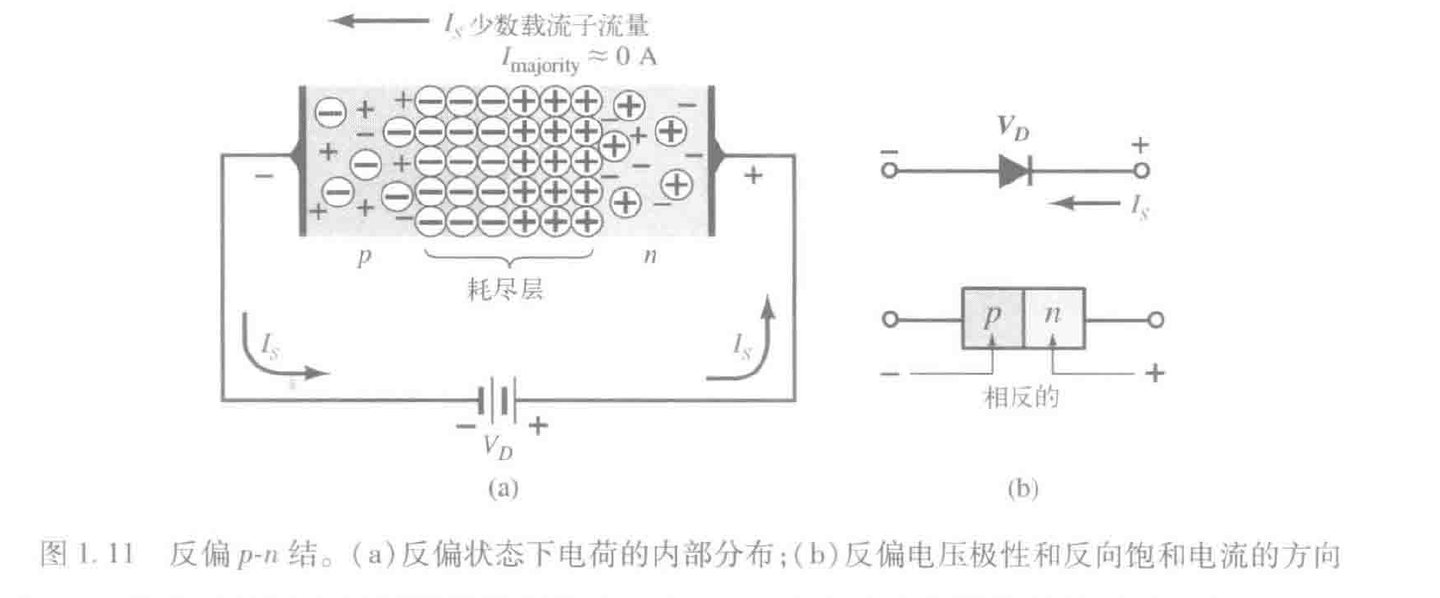
当将电压反向加在PN结上(正极接N,负极接P)时,P型半导体中的空穴和N型半导体中的电子被外加电压吸引,使得P型半导体中的负离子和N型半导体中的正离子急剧增多,导致耗尽层加宽,加宽到了多子无法通过耗尽层,如上图所示。
但是,外加电场并未影响到少子,少子进入耗尽层的数量仍然不变,与无偏置情况下的数量相同。
反向饱和电流用$I_{S}$表示。
正向偏置
当讲电压正向加在PN结(正极接P,负极接N)上时,外加电压将会吸引P型半导体的阴离子和N型半导体的阳离子,使得耗尽层变窄。随着外加电压的变大,耗尽层变得更窄,更多的多子可以通过PN结,这将导致电流呈指数级增长。
对于少子而言,耗尽层宽度的下降使得P型半导体中的电子和N型半导体中的空穴流进对方的区域
二极管的一般特性
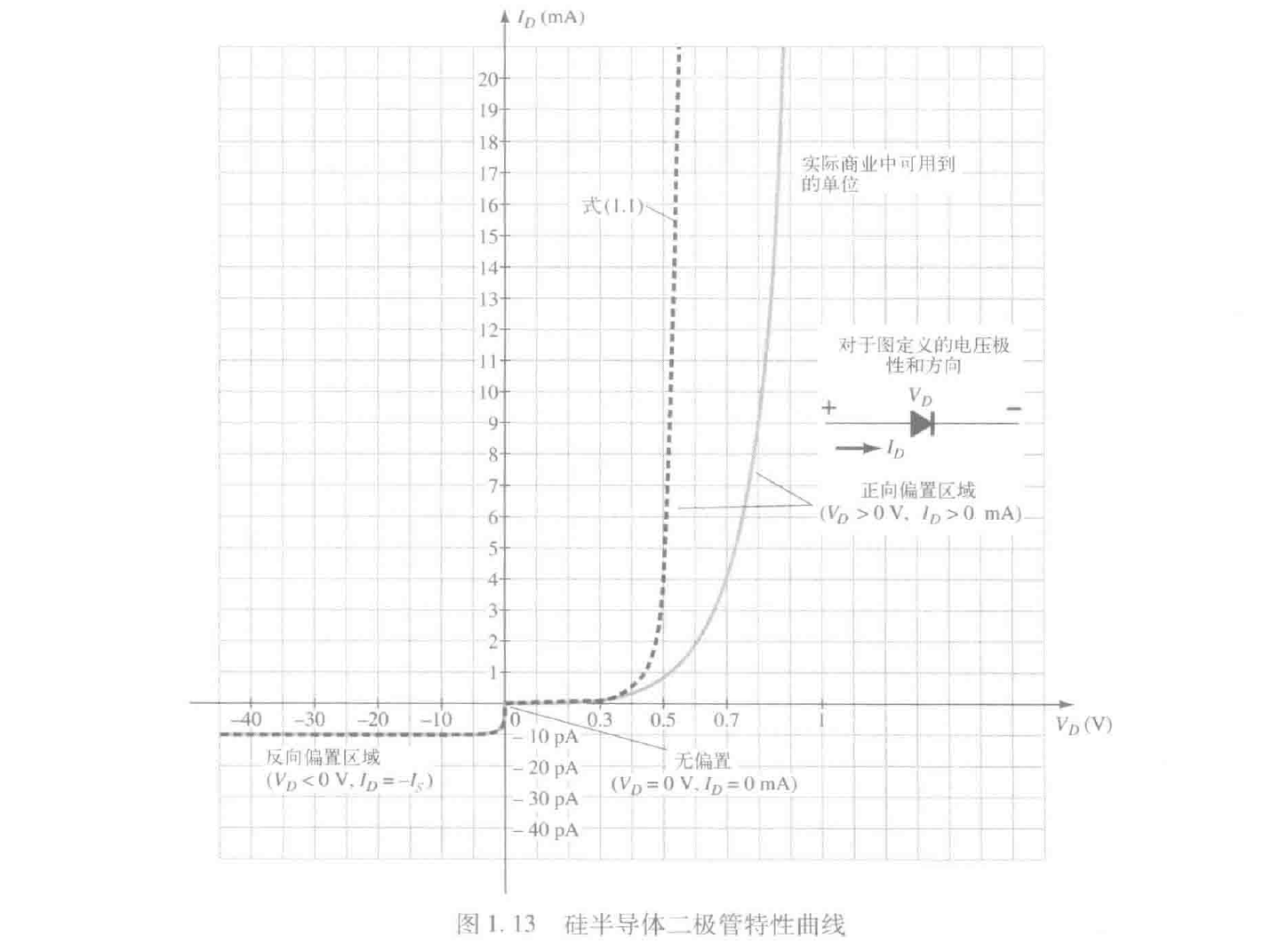
一般特性
我们使用肖克利方程来描述半导体二极管的一般特性
$$
I_{D}=I_{S}(e^{\frac{U_D}{nU_T}}-1)
$$
其中,$I_D$是通过二极管的电流,$I_{S}$是反向饱和电流,$U_{D}$是加在二极管上的正偏电压,$n$是影响因子,范围在1~2之间,但除非特殊说明,否则都按1处理。
我们定义$U_{T}$是热电压,由下式决定
$$
U_{T}=\frac{kT}{q}
$$
其中,$k$是玻尔兹曼常数,为$1.38 \times 10^{-23}J/K$,T是热力学温度,q是电子的电荷量,为$1.6\times 10^{-19}C$。
整理得$$
I_D=I_S,e^{\frac{qU_D}{kT}}-I_S
$$
对其分析,明显得:
- $U_D<0$时,当$U_D$趋于负无穷时,$e^{\frac{qU_D}{kT}}$趋于零,此时$I_D$几乎等于$-I_S$,在图中对应反向偏置区域。
- $U_D>0$时,式中的指数部分将快速增长并超过第二部分,图中曲线随者电压的增大而趋向于垂直。
但是,在实际的元件中,反向饱和电流通常会比肖克利方程中的$I_S$大得多,这是因为一些没有包含在肖克利方程中的因素引起的,譬如耗尽区载流子的产生以及表面漏电流。
此外,pn结的接触面积与反向饱和电流的大小有着直接的对应关系。
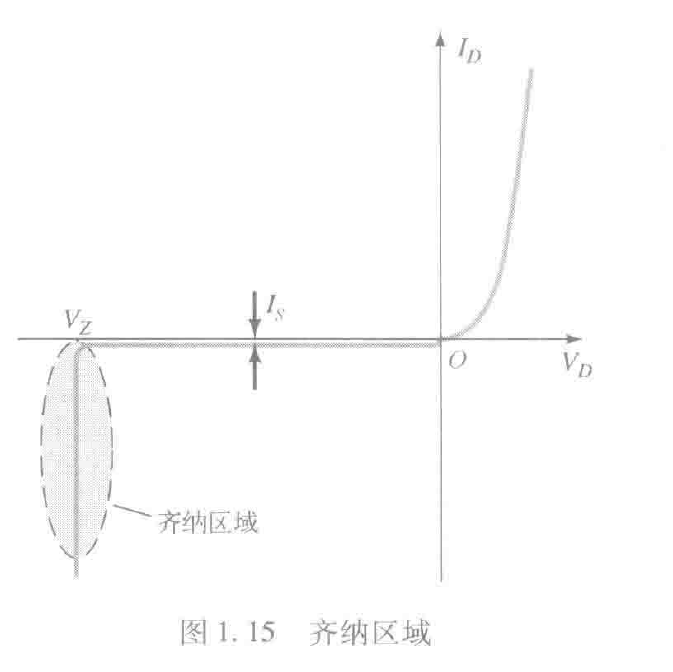
齐纳区域
双极性晶体管(Bipolar Junction Transistor)
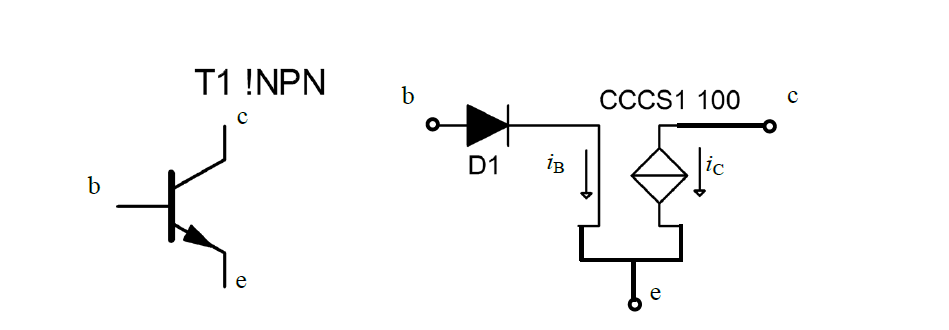
三极管其电路符号如图所示,一共有三个引脚,分别为基极(Base),集电极(Collector)和发射极(Emitter)。
注意,带箭头的引脚即为发射极,箭头向外的为NPN型,相反即为PNP型。
图示右侧给出了等效电路关系,其本质上是一个$CCCS$,对于NPN管,若发射极电流是流出的,则基极和集电极电流是流入的,PNP则相反
对于NPN管,我们定义发射结电压为其基极电压与发射级电压之差,即
$$
u_{BE}=u_B-u_E
$$
此值为正时才能使基极与发射级时导通关系。
根据图中给出的等效电路关系,由基尔霍夫定律与受控源规律,我们有:
$$
\begin{equation}\begin{split}
i_B+i_C=&i_E \
i_C=& \beta i_B
\end{split}\end{equation}
$$
其中,$\beta$是电流放大倍数。
伏安特性曲线
输入伏安特性
BJT的输入伏安特性是指其基极电流$i_B$与发射结电压$u_{BE}$的关系,其可能受到$u_{CE}$的影响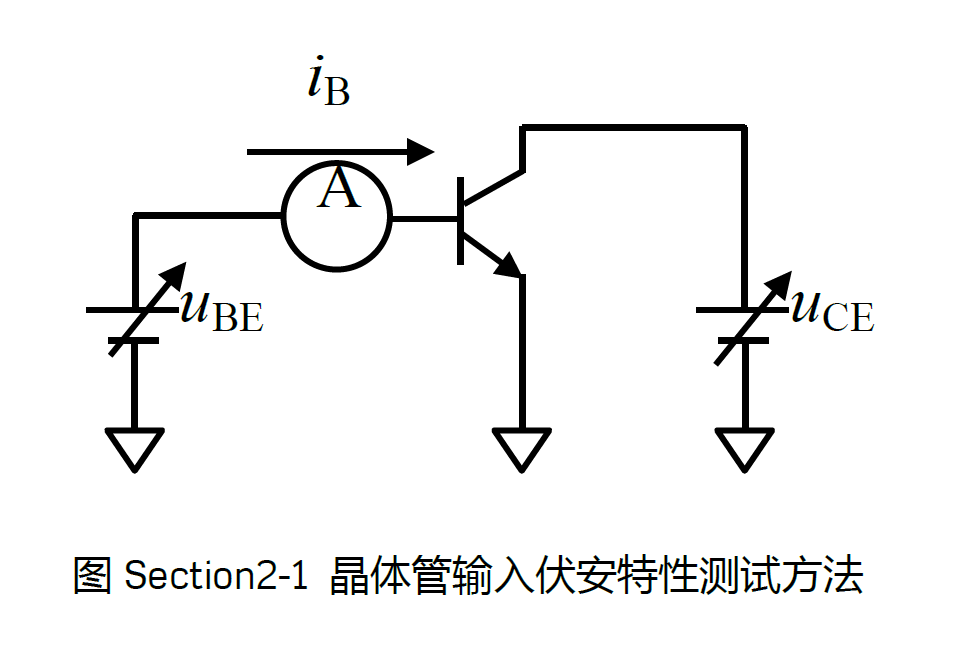
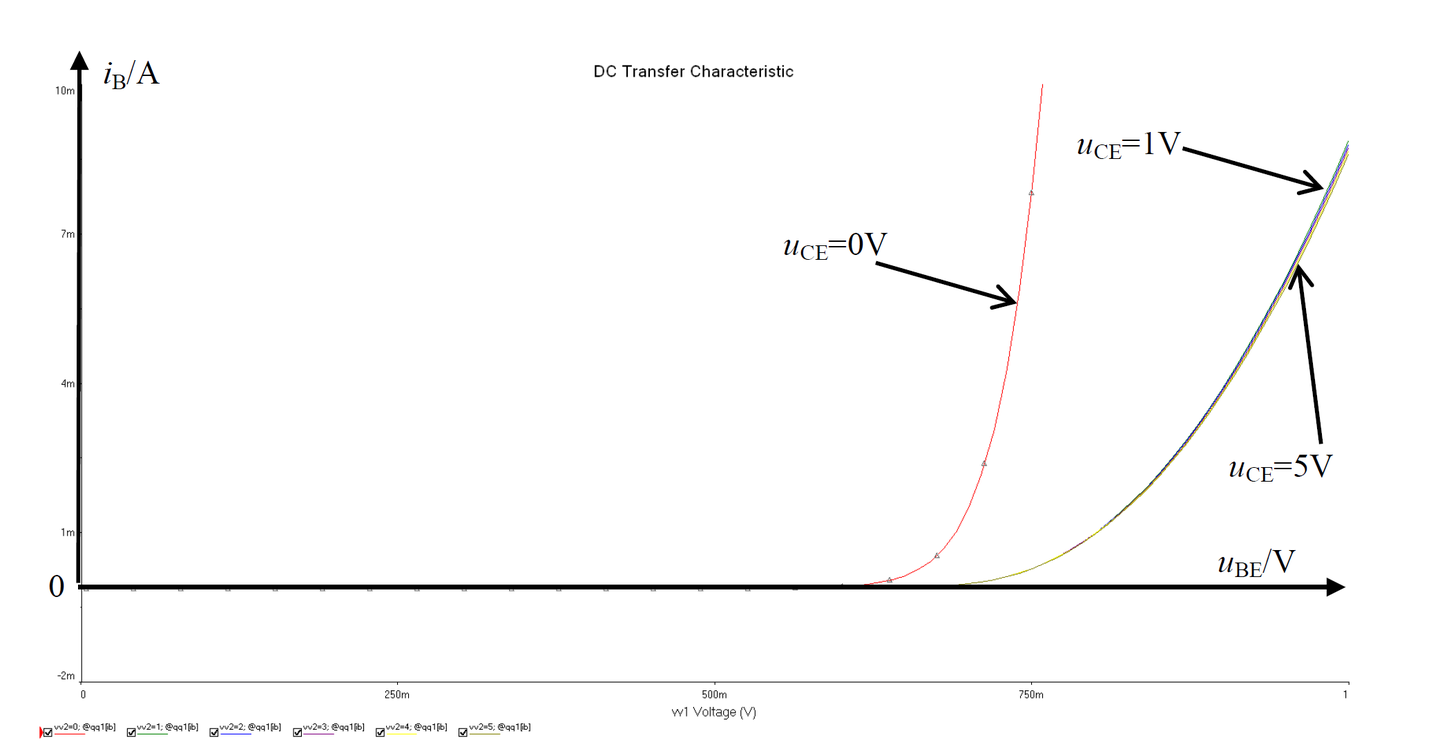
如图所示,除$u_{CE}=$比较特殊外,其余曲线基本重合——称为一簇线,即为晶体管的输入伏安特性,可使用如下表达式近似表述:
$$
i_B=I_S(e^{\frac{u_{BE}}{U_T}}-1)
$$
其中,$u_T$是热电压,是一个与绝对温度成比值的值,27℃时约为26$mV$,$I_S$是反向饱和电流,虽然每个晶体管的值都不同,但很小,当$u_{BE} \rightarrow +\infty$时,明显$i_B \rightarrow -I_S$。
一般的,当$u_{BE}>0.7V$时,基极开始出现较为明显的电流。
输出伏安特性
输出伏安特性是指在一个确定的基极电流下,集电极电流$i_C$与$u_{CE}$的关系。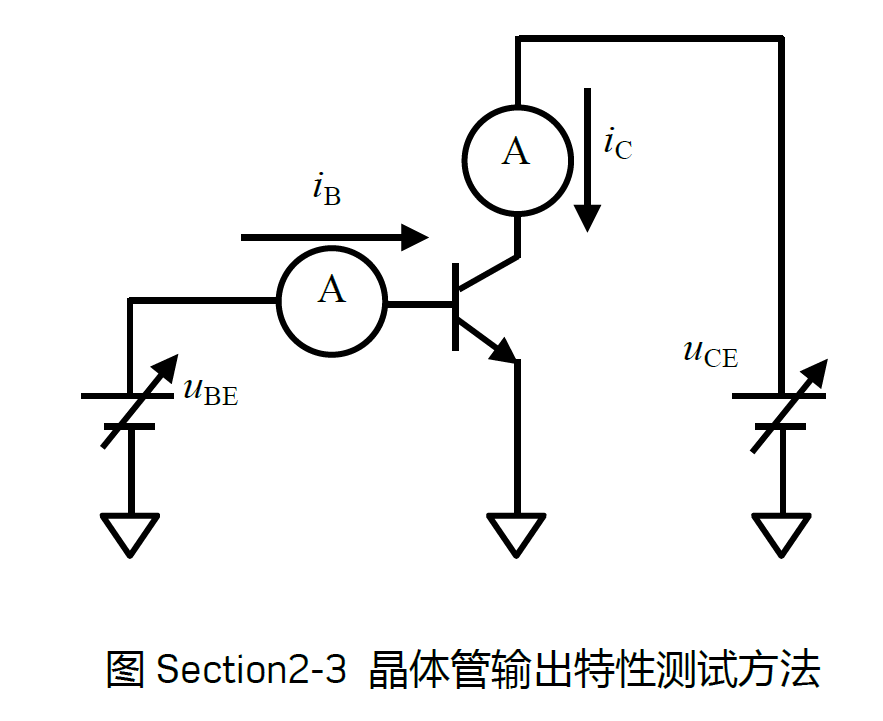
在理想情况下,集电极电流应该只与基极电流成正比,但是现实情况是: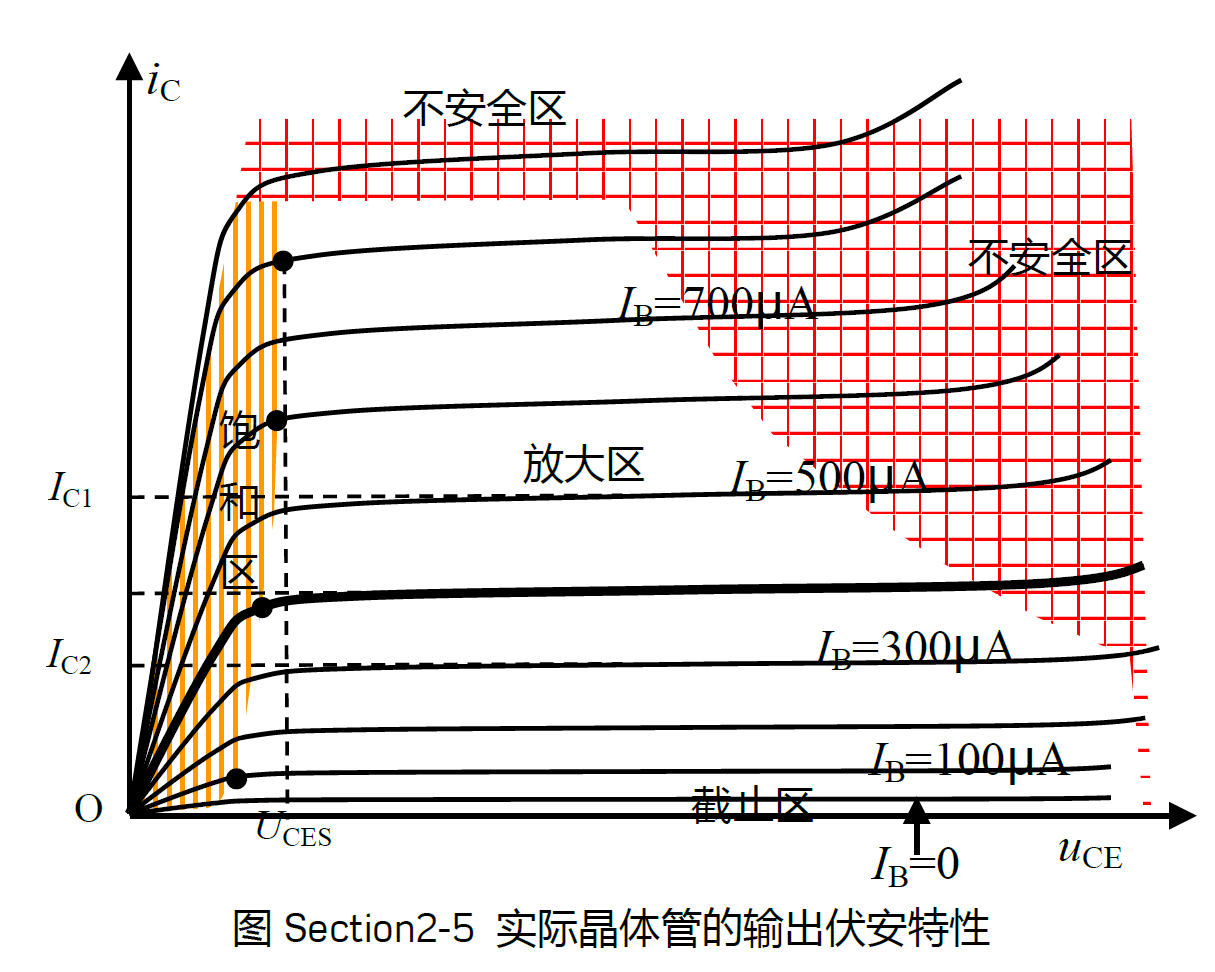
输出区域划分
- 放大区
在放大区中,图中曲线为微微上翘的平直曲线,在此区域内,集电极电流几乎不受$u_{CE}$控制,近似满足下式:
$$
i_C=\beta i_B
$$ - 饱和区
图中的左侧区域,在此区域内,集电极电流随着$u_{CE}$的增大而增大。
我们定义$U_{CES}$为晶体管的饱和压降,是饱和区和放大区的分界电压,一般认为约为0.3V,但显然,随着$i_B$的上升,饱和压降也会上升 - 截止区
当基极电流为零时,集电极电流并不为零,而是存在与$u_{CE}$相关的漏电流。我们定义$I_B=0$时的区域为截止区,其含义为晶体管处于几乎没有电流进出的状态,就像完全关闭一样。

