背景

在机器人控制领域中，电机是一个重要的组成部分，无论是三轴云台、机械臂还是AGV，电机都在其中起到了动力输出的作用，常规的有刷电机结构简单，在实际工程中有着广泛的应用，但在机器人的运动控制中，有刷电机体现出了其控制精度不高和寿命短的缺陷，因此并未在机器人控制领域中广泛应用，而无刷电机虽然制造成本更高，但是其控制精度、可靠性和寿命会比有刷电机更加优越，被广泛应用在了机器人领域中。

通常无刷电机分成两个使用场景，第一种的典型应用场景是在无人机上，其转速非常高，对位置或力矩的控制基本没有要求，而另一种则在机器人上，转速通常最大在几百rpm，但是对位置和力矩的控制精度要求非常大，因而在驱动和控制方法上分成了几种不同的派系：

在高速运动场景下，可以使用无感开环控制，因其对力矩没有要求，可以使用方波进行驱动，这种设计硬件结构十分简单，只需要控制栅极驱动器的通断，换向时只需要判断电机反电动势是否过零点，过零点即可进行换向操作。但这种方法的缺点是低速和启动性能比较差，而且噪声非常大，不适合用在精细控制领域中。
在低速高精度控制场景下，无刷电机更多采用FOC（Field-Oriented Control）进行控制，FOC被称为磁场导向控制，是一种利用变频器（VFD）控制三相交流电机的技术。这种技术通过调整变频器的输出频率、输出电压的大小及相位，来控制电机的输出。其特性是可以单独控制电机中每个绕组线圈的磁场方向和强度，类似他励式直流电机。由于在FOC算法的方程式中，三相交流电机的定子电流通过两个可视化的正交矢量分量来描述，因此这种控制方法又被称为矢量控制（Vector Control）。FOC方法可用于控制交流感应电机和直流无刷电机。最开始出现这种控制方法，就是为了提高电机的性能。在FOC控制下，电机不仅能在全速范围内平稳运行，以零速度产生额定扭矩，还具备良好的高速动态性能，如能够做到快速地加速或减速。

因此，FOC的独特速度和力矩性能使得其成为了近些年来最常出现的电机控制算法，了解其对应的控制原理能够更好控制无刷电机，还可将其封装为伺服模块，大大增强了易用性。

无刷电机原理

以三相二极内转子电机为例，定子的三相绕组有星形联结方式和三角联结方式，而三相星形联结的二二导通方式最为常用，这里使用该模型做简单讨论：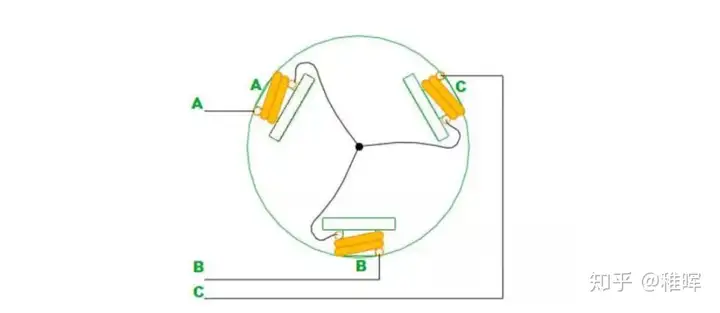

如图所示，电机的三个线圈的一头均连接至中心点$O$（中心为转子，是永磁体，未画出），如果此时在AB相上通电，容易根据右手螺旋定则得出此时线圈产生的合磁场方向与$OB$成$30°$角，$N$极指向右下方，而此时，内转子受到磁场作用的力，会使得内转子的永磁铁的磁链和线圈的磁链相垂直。此时电机也就完成了一次$60°$转动，依次类推，分别在三相的两相上一次通电，也就“牵动”电机完成了一次完整旋转。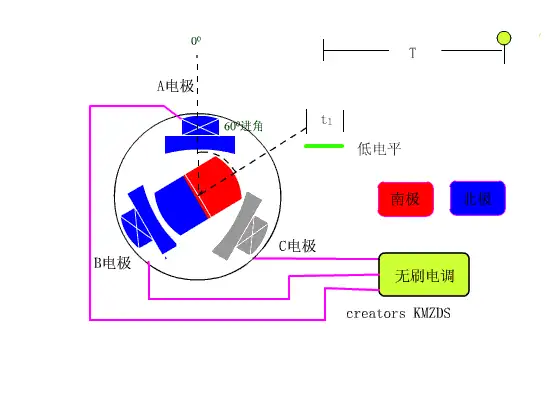

而我们需要对换向进行操作，则需要栅极驱动器和MOS管。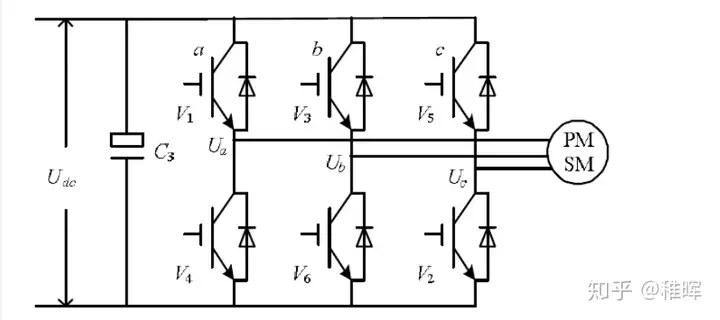

上图显示出了需要驱动无刷电机转动的三相逆变电路（图中的功率器件其实是IGBT），通过开关不同的MOS管，就能够实现对不同相和不同方向的通电和断开处理，进而也就实现了无刷电机的转向和换相。

栅极驱动器，顾名思义，是驱动栅极使得MOS管打开的芯片。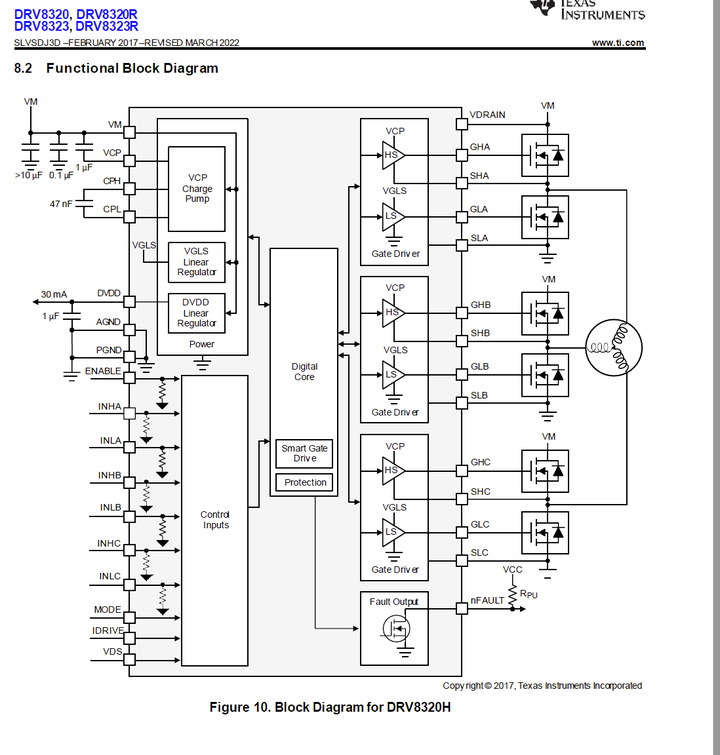

上图是Ti的智能栅极驱动芯片，带上了许多保护功能，如过压保护和过流保护等，但最核心的还是框图中的Gate Driver（栅极驱动器），芯片接收来自控制器的PWM信号，高电平占周期的时长决定了MOS管的开通时长，两个MOS管相连的电路我们称之为半桥电路，如图所示，三相电机的线圈的引头连接至桥臂中央，这也是容易理解的。

三相电机的旋转波形与驱动波形

将示波器的探头连接至电机三相中的两相，如果是三通道的则更好，我们最后应该会得到三个正弦曲线，幅值相同而相邻波形相位差为$120°$。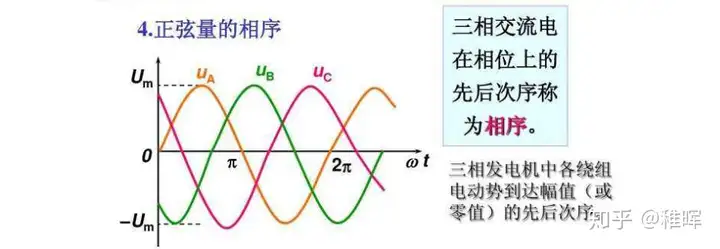

用手去旋转电机，是能够感受到强烈的阻尼感，我们上面的分析表明，转子在磁场中只有六个稳定的状态，因此在整个的旋转过程中是不平滑的，为了解决这个问题，也顺带衍生出了无刷电机中PMSM和BLDC的区别。

BLDC的解决方式比较直白，既然我转一圈要切换六次，那么就增加电机的极对数，增加的极对数越多，我一圈当中就会切换12次甚至更多，这样“颗粒感”就会变的更小，切换的时间和间距越短，电机的运行效果就越平滑。

上图是一个极对数为9的无刷电机，但是电机仍然只有三根线在外面。

但是，即使我们增加了极对数，但是仍然没有解决根本上的问题，因为方波本身是不平滑的，而无刷电机的波形确实正弦波形，那就直接用正弦波去驱动不就行了？没错，这就是PMSM的解决方式，其反电动势被人为设计成正弦波的形状，我们再搭配一些软件和算法，把方波的驱动信号转换被SPWM正弦波或者SVPWM马鞍波，这样就从根本上解决了这个问题，这也就是FOC的实现原理。

FOC控制原理

我们先在控制系统的顶层来了解一下控制流程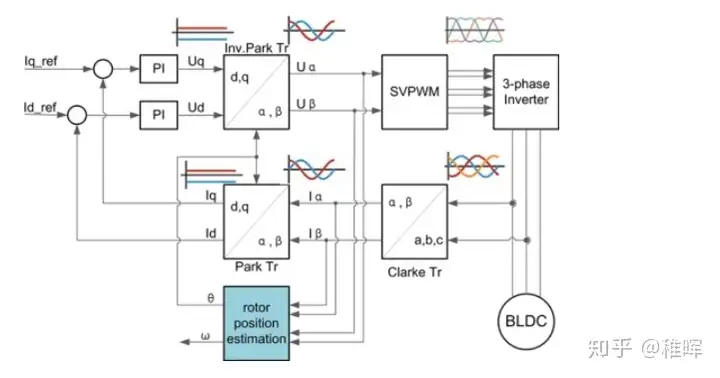

上图中是电流闭环控制，也就是恒定力矩模式。整个控制流程是这样的：

对电机三相电流进行采样得到 $𝐼_𝑎,𝐼_𝑏,𝐼_𝑐$
将 $𝐼_𝑎,𝐼_𝑏,𝐼_𝑐$ 经过$Clark$变换得到 $𝐼_𝛼,𝐼_𝛽$
将 $𝐼_𝛼,𝐼_𝛽$经过$Park变换$得到 $𝐼_𝑞,𝐼_𝑑$
计算$𝐼𝑞,𝐼_𝑑$和其设定值$𝐼{𝑞_{𝑟𝑒𝑓}},𝐼_{d_{𝑟𝑒𝑓}}$,的误差
将上述误差输入两个PID控制器，得到输出的控制电压 $𝑈_𝑞,𝑈_𝑑$
将$𝑈_𝑞,𝑈_𝑑$进行反Park变换得到 $𝑈_𝛼,𝑈_𝛽$
用$𝑈_𝛼,𝑈_𝛽$合成电压空间矢量，输入$SVPWM$模块进行调制，输出该时刻三个半桥的状态编码值（前文有提到）
按照前面输出的编码值控制三相逆变器的$MOS$管开关，驱动电机
循环上述步骤

Clark变换

对于三相电机而言，由KCL很容易得到

$$
I_a+I_b+I_C=0
$$
定义三相坐标系如图所示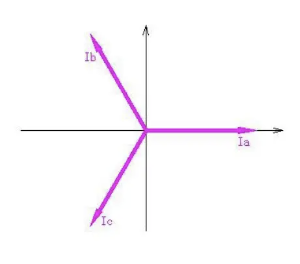

这和我们之前转动电机得到的相位差结果基本一致，但是他有三个轴，分析起来太麻烦了，我们通过定义正交基向量来重新定义一个$\alpha-\beta$坐标系
$$
\left{\begin{array}{l}
I_{\alpha}=I_{a}+\cos \left(\frac{2 \pi}{3}\right) I_{b}+\cos \left(\frac{2 \pi}{3}\right) I_{c} \
I_{\beta}=\sin \left(\frac{2 \pi}{3}\right) I_{b}-\sin \left(\frac{2 \pi}{3}\right) I_{c}
\end{array}\right.
$$
相当于把原来的三个向量投影到坐标轴上，只需要控制两个变量了就能达到原来的效果，但是我们新坐标系下仍然是以正弦方式在做变化的，我们希望把它线性化，这样更容易控制和计算，也就引入了Park变换。

Park变换

为什么上面经过Clark变换的结果是正弦变化的呢？因为电机本身是在旋转的，我们需要消除“旋转”这一特征才能达到线性化的目的。
在Park变换中，我们将坐标系逆时针旋转$\theta$°，定义$\theta$为电机转子转过的角度，就像图片的这样。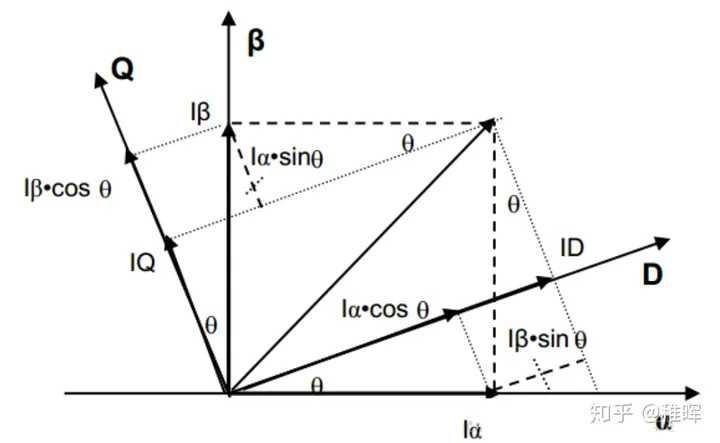

坐标变换的结果仍然是简单的矢量投影，公式如下：
$$
\left{\begin{array}{l}
I_{d}=I_{\alpha} \cos (\theta)+I_{\beta} \sin (\theta) \
I_{q}=-I_{\alpha} \sin (\theta)+I_{\beta} \cos (\theta)
\end{array}\right.
$$
转子转多少度那么$d-q$坐标系就转多少度，因此，“旋转”的特征被消除，我们对电机的控制最后解耦为对$I_d,I_q$的控制，也就可以搭配PID这种线性控制器来控制了。

PID控制

FOC控制中主要会用到几个控制环路，分别是电流环，速度环，位置环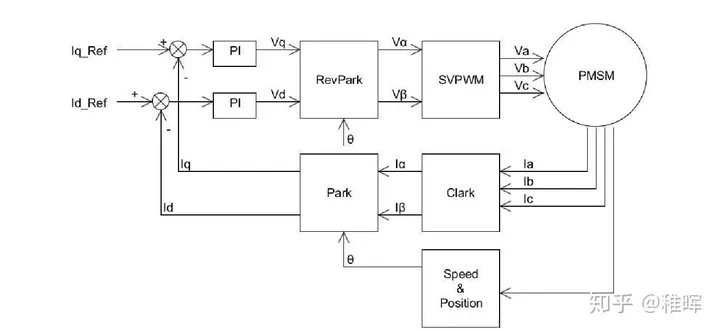

我们首先讨论电流环，在$d-q$坐标系中，我们讲到在这个坐标系下消除了”旋转“的特征，两个向量对于转子而言分别是径向向量和切向向量，很明显，推动转子旋转的向量就是切向向量，而径向向量是我们不需要的，如果它不为0就会影响效率和力矩，因此我们希望把它控制为0，因此电流环的作用就是使径向电流尽可能为0（0就是控制器的期望），而使切向电流达到期望值。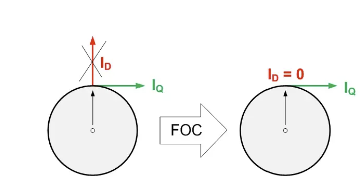

电流环的控制作用到这里就结束了，它负责的东西就这么多。

速度环和位置环

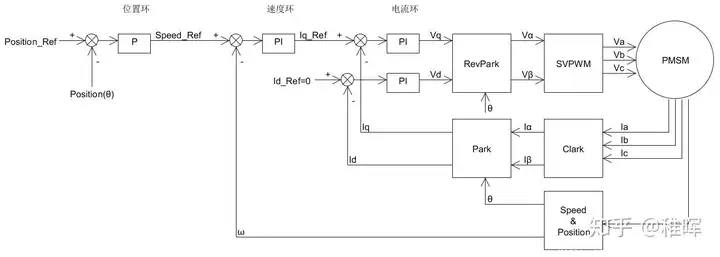
其实在了解电流环之后剩下的两个环不难理解，这里不再赘述。
至此整个控制环节基本结束，但是我们注意到电流环的输出线给到了RevPark变换先还原到$\alpha-\beta$坐标系下，但是却没有RevClark变换，而是转到了一个叫做SVPWM的东西，它的输出是三相每一相的电压。

SVPWM

全称Space Vector PWM，也是PWM，但是加上了空间电压矢量的前缀，我们首先把SV搞明白。

Space Vector

我们不妨先把线圈通电，就像图中这样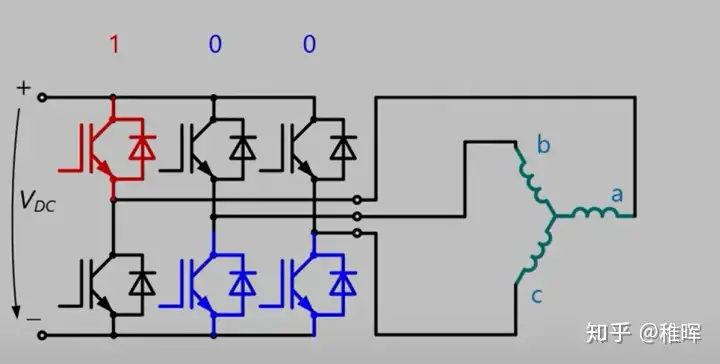

我们假设每个线圈的电阻都是相同的，我们可以得到这样一个电路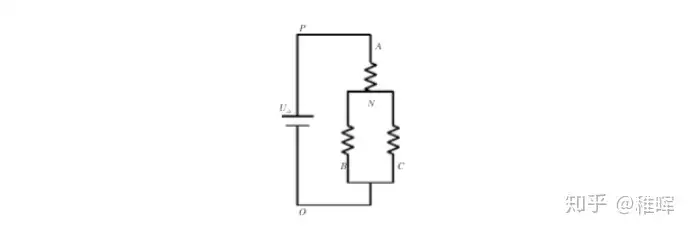

这是非常简单的一个分压电路，容易计算得出各相的相电压
$$
\begin{array}{l}
U_{a}=U_{A}-U_{N}=\frac{2}{3} U_{d c} \
U_{b}=U_{B}-U_{N}=-\frac{1}{3} U_{d c} \
U_{c}=U_{C}-U_{N}=-\frac{1}{3} U_{d c}
\end{array}
$$
各相电压的方向是和电流方向相同的，我们规定正方向是指向中心的方向的话，就能得到这么一幅图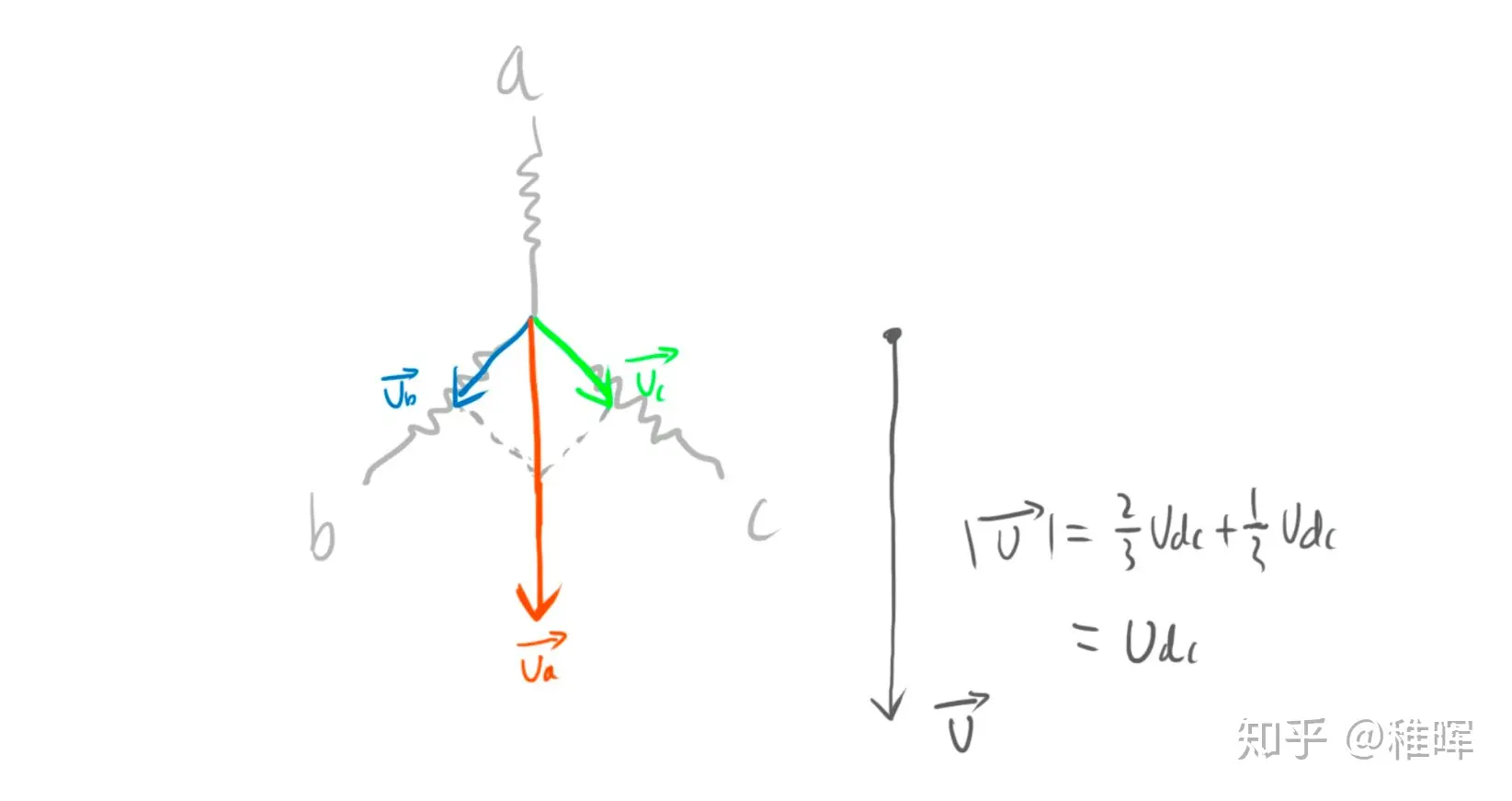

这个合成的向量是$AO$方向的，由右手螺旋定则能看出其$N$朝向下方，而根据我们前面的分析，转子会努力转到这个方向上来，也就是说，SpaceVector代表了转子的方向（或者电机角度），而改变电机转子的角度就需要去改变空间电压矢量的方向，而空间电压矢量本质上来说，是半桥的不同开关状态导致了各相电压的不同，进而影响了空间电压矢量的位置。

我们定义一个开关函数$S(x)$用来描述半桥开关时的状态
$$
S(x)=\left{
\begin{aligned}
1&,上桥臂导通\
0&,下桥臂导通
\end{aligned} \right.
$$
注意：在一个开关动作中，上下桥臂不能同时开启，同时开启则意味着短路，为此还需要引入死区时间控制来保证这一点。
对于三相电机而言，$(S_a,S_b.S_c)$的组合为八个，去掉两个零矢量（0,0,0）和（1,1,1）(去掉的原因是这两个状态线圈时没有电流的，不产生力矩)，剩下的六个空间电压矢量能明显的看出来和之前的六步换向很像。我们如果想让一个空间电压矢量去旋转的任意方向，就需要对六个空间电压矢量去进行合成，也就是SVPMM技术。

SVPWM

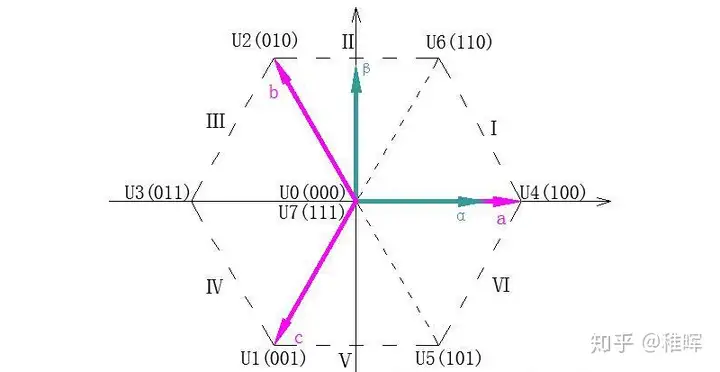
为了简便处理，我们不会使用六个矢量去合成，能看到这六个矢量把整个空间分成了六个扇区，我们会首先判断矢量所在扇区的位置，然后用扇区的两个电压矢量去合成扇区内的任意电压矢量，即有
$$
U_{ref}\cdot\ T=U_x \cdot T_x+U_y \cdot T_y+U^*0 \cdot T_0^*
$$
公式中，$T$是一个PWM周期，$T_x,T_y,T_0^*$都是对应矢量的作用时间，插入零矢量会让空间电压矢量切换的更加顺滑。
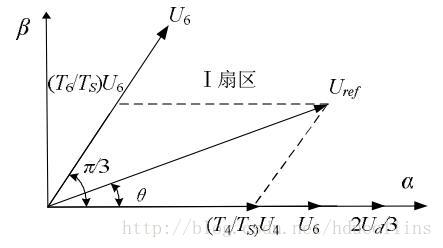
比如说，我们要在扇区$I$内去合成一个指定角度的空间电压矢量$U{ref}$

由正弦定理有
$$
\frac{\frac{T_6}{T}U_6}{\sin \theta}=\frac{\frac{T_4}{T}U_4}{\sin (\frac{\pi}{3}-\theta)}=\frac{U_{ref}}{\sin \frac{2\pi}{3}}
$$
能计算出
$$
\begin{aligned}
T_4&=mT\sin(\frac{\pi}{3}-\theta)\
T_6&=mT\sin\theta
\end{aligned}
$$
剩余时间则分配给零矢量，至此，整个FOC的控制部分就全部结束了，但我们还有一个问题，虽然理论上来说，只要这个电压矢量的时间持续的够长，这六个开关怎么开关都行，但是开关对于MOS是有损耗的，我们希望尽可能减少开关的次数，因此有了下面的切换顺序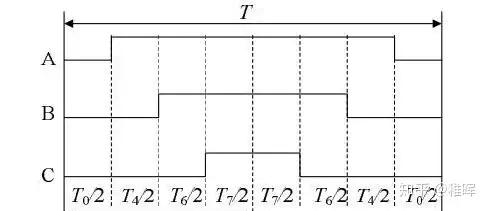

我们在实际中会把PWM配置成中心对齐模式，在这种开关控制模式下，每一次都只会开关一次，而零矢量被分配在了起始和中间位置，有效降低了开关次数的同时也就降低了PWM的谐波分量。同理也可以列出其他扇区的切换顺序。

至此，整个FOC的九个步骤全部完成.