第一题

% 定义自然频率
wn = 2;

% 定义阻尼比数组
zeta_values = [0, 0.25, 0.5, 1.0, 2.0];

% 创建一个图形窗口
figure;
hold on;

% 绘制每个阻尼比的响应曲线
for i = 1:length(zeta_values)
    zeta = zeta_values(i);
    % 定义传递函数
    sys = tf(wn^2, [1, 2*zeta*wn, wn^2]);
    % 绘制单位阶跃响应
    step(sys);
end

% 添加图例和标题
legend('zeta=0', 'zeta=0.25', 'zeta=0.5', 'zeta=1.0', 'zeta=2.0');
title('单位阶跃响应 - 不同阻尼比');
xlabel('时间 (s)');
ylabel('响应');
grid on;
hold off;

屏幕截图 2024-12-20 231823.png

阻尼比 $\zeta$：
$\zeta = 0$：系统无阻尼，表现为持续振荡。
$0 < \zeta < 1$：系统为欠阻尼，表现为振荡逐渐衰减。
$\zeta = 1$：系统为临界阻尼，快速达到稳态，无振荡。
$\zeta > 1$：系统为过阻尼，响应缓慢，无振荡。

第二题

% 定义阻尼比

zeta = 0.25;

% 定义自然频率数组

wn_values = [1, 2, 4, 6];

% 创建一个图形窗口

figure;

hold on;

% 绘制每个自然频率的响应曲线

for i = 1:length(wn_values)

wn = wn_values(i);

% 定义传递函数

sys = tf(wn^2, [1, 2*zeta*wn, wn^2]);

% 绘制单位阶跃响应

step(sys);

end

% 添加图例和标题

legend('wn=1', 'wn=2', 'wn=4', 'wn=6');

title('单位阶跃响应 - 不同自然频率');

xlabel('时间 (s)');

ylabel('响应');

grid on;

hold off;

屏幕截图 2024-12-20 231946.png

自然频率 $\omega_n$：
增加 $\omega_n$会加快系统响应速度。
$\omega_n$ 越大，系统达到稳态的时间越短。

2.请绘制下面单位负反馈系统的根轨迹曲线
（可自行设计开环传递函数）在MATLAB中采用根轨迹法求取使得闭环系统稳定的K值的范围。

% 定义传递函数的分子和分母

numerator = [1]; % K 是可变的，因此初始设置为 1

denominator = conv([1, 0], conv([1, 2, 2], [1, 6, 13]));

% 创建传递函数

sys = tf(numerator, denominator);

% 绘制根轨迹

figure;

rlocus(sys);

title('根轨迹');

xlabel('实部');

ylabel('虚部');

grid on;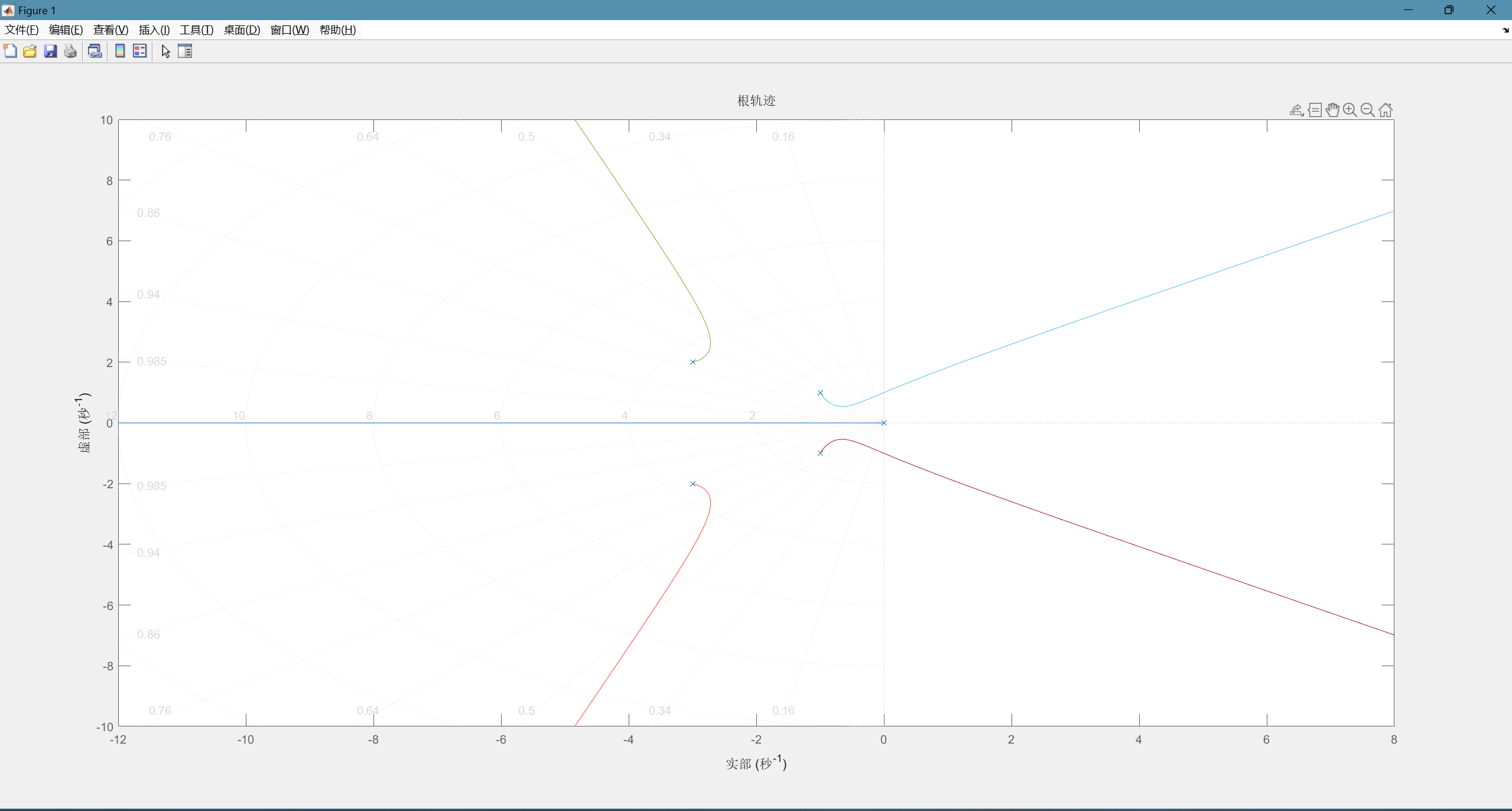

% 定义传递函数的分子和分母

numerator = [1]; % K 是可变的，因此初始设置为 1

denominator = conv([1, 0], conv([1, 2, 2], [1, 6, 13]));

% 创建传递函数

sys = tf(numerator, denominator);

% 计算根轨迹

[r, k] = rlocus(sys);

% 初始化稳定性范围

k_stable_min = Inf;

k_stable_max = -Inf;

% 遍历根轨迹数据，寻找稳定的 K 值范围

for i = 1:length(k)

poles = r(:, i);

if all(real(poles) < 0) % 检查所有极点是否在左半平面

k_stable_min = min(k_stable_min, k(i));

k_stable_max = max(k_stable_max, k(i));

end

end

% 输出稳定的 K 值范围

fprintf('稳定的 K 值范围: %.2f <= K <= %.2f\n', k_stable_min, k_stable_max);

第三题

% 定义传递函数的分子和分母

numerator = [1, 0.125];

denominator = conv([1, 0, 0], conv([1, 5], conv([1, 20], [1, 50])));

% 创建传递函数

sys = tf(numerator, denominator);

% 打开根轨迹设计工具

rltool(sys);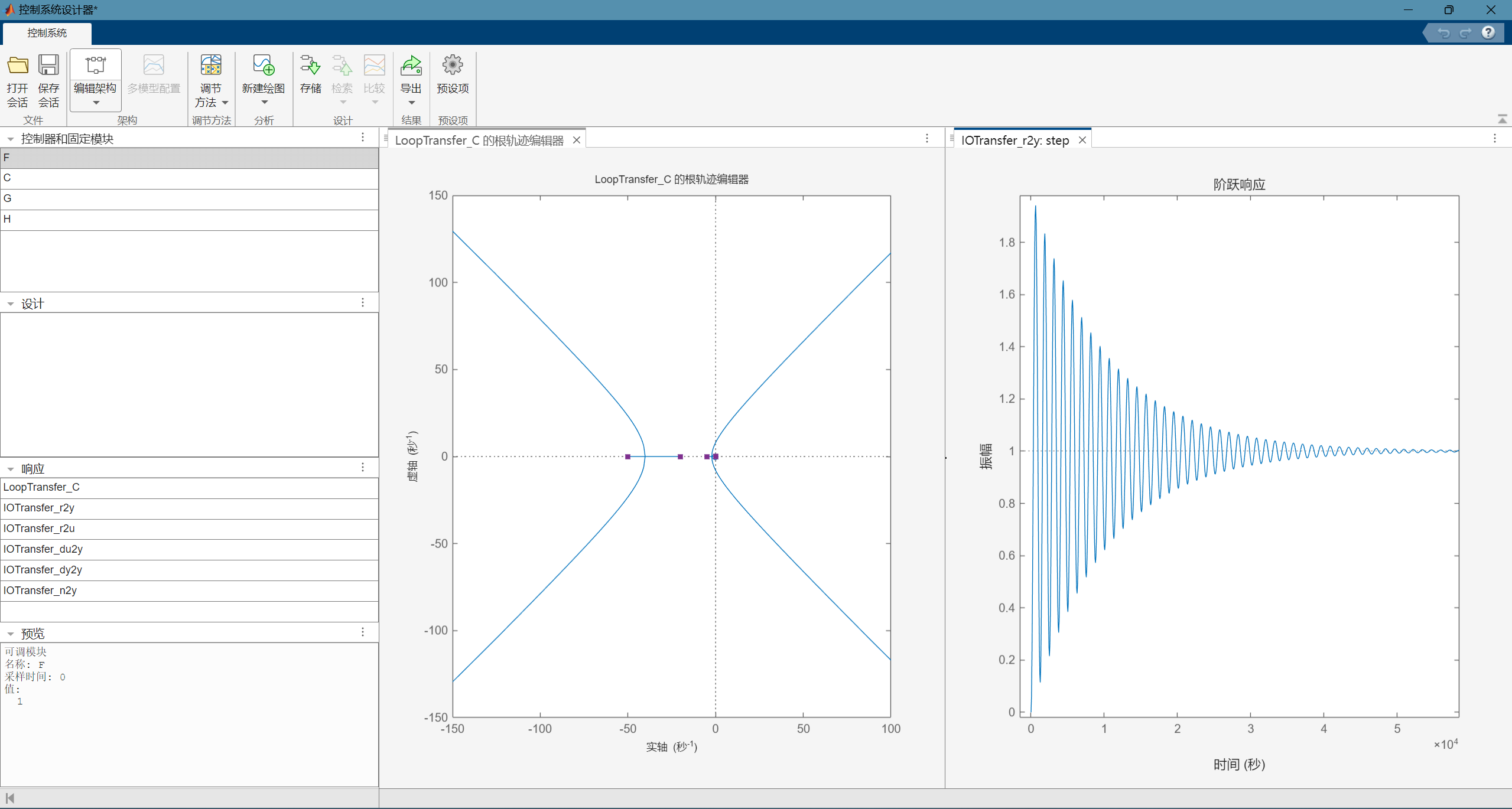

添加一个实零点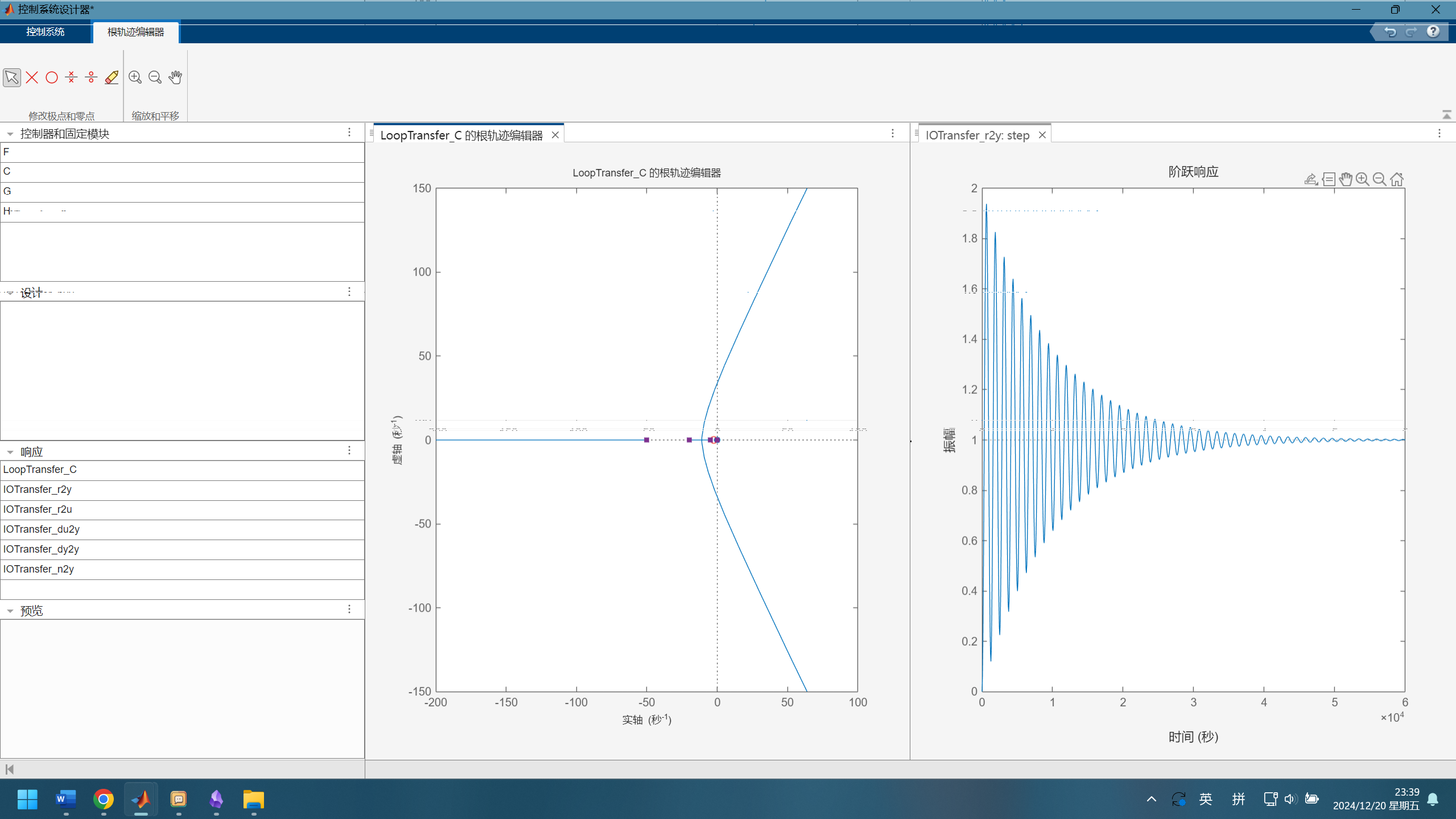

第四题

屏幕截图 2024-12-20 234221.png
屏幕截图 2024-12-20 234252.png

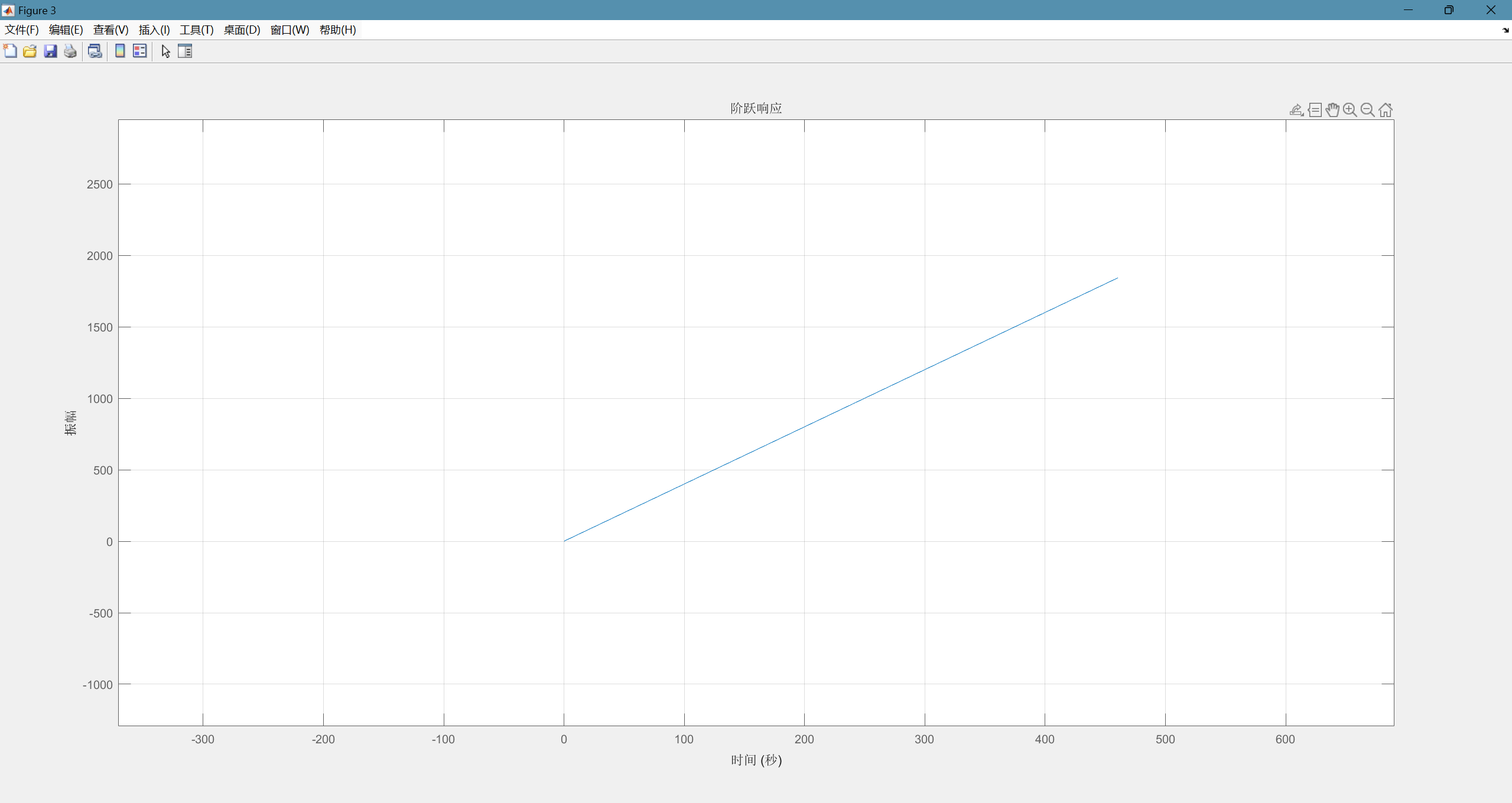
相位裕度和增益裕度都为正，Nyquist曲线不包围-1，系统稳定

第五题

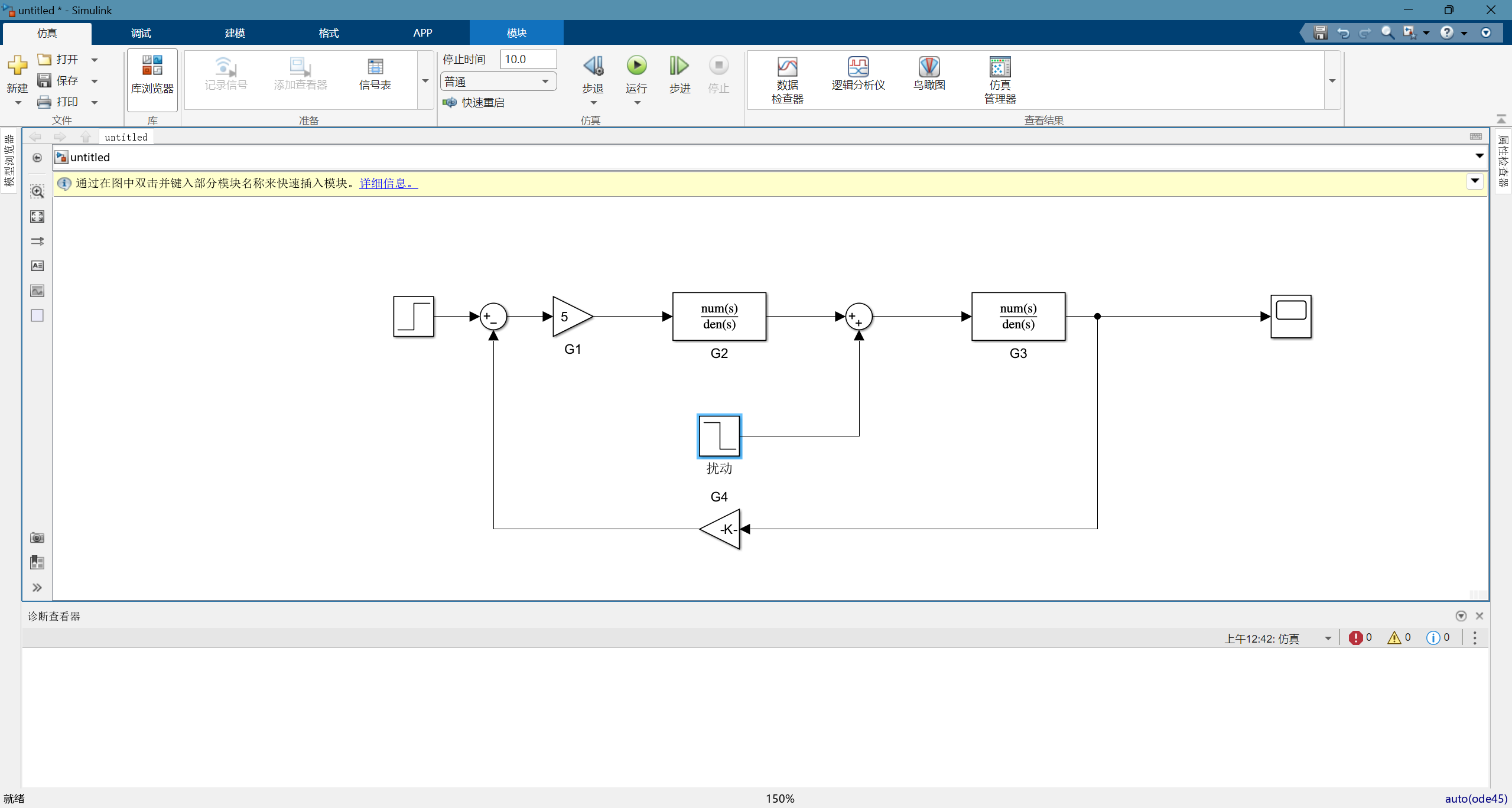
各component配置，如下图所示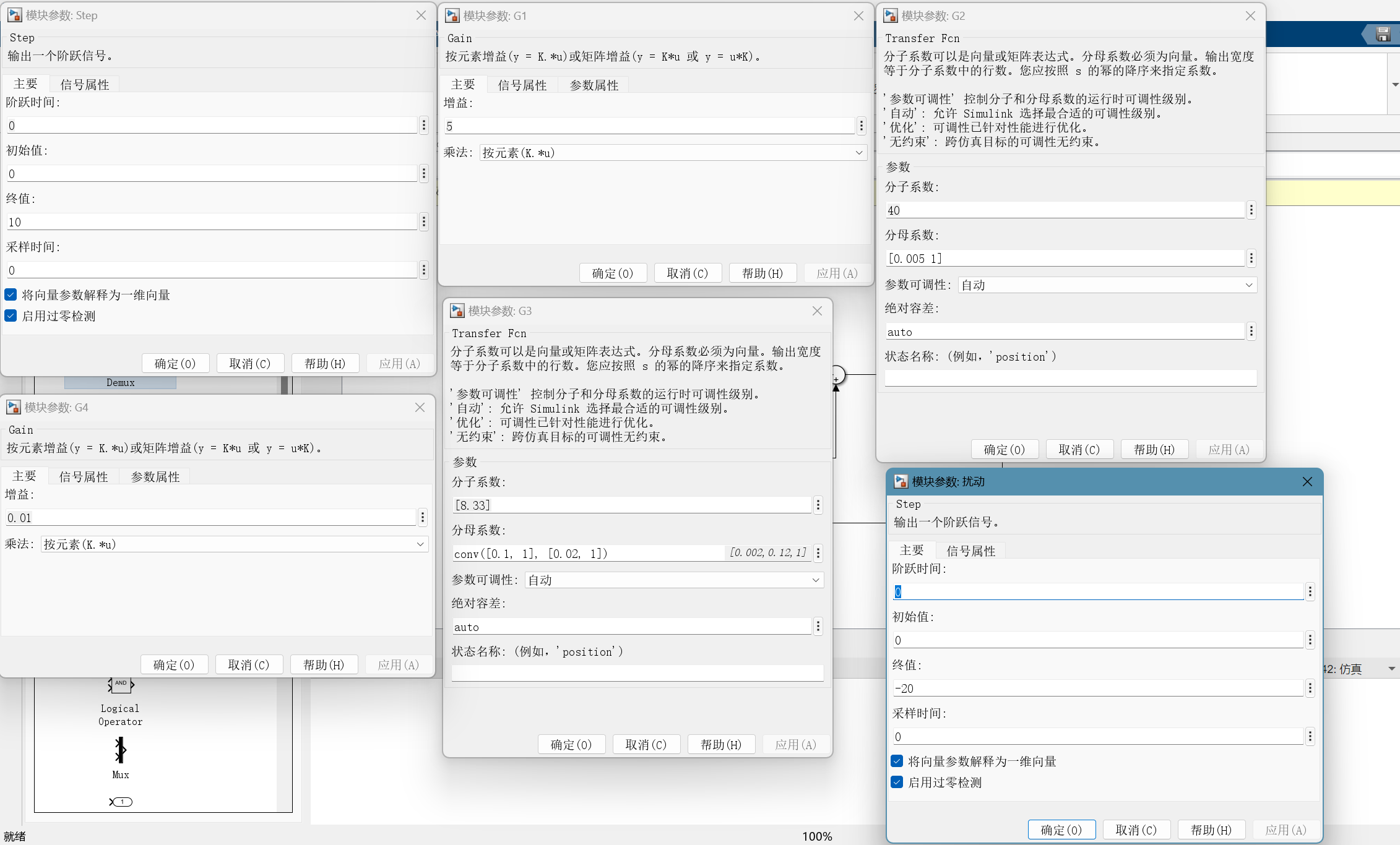

系统输出如下图所示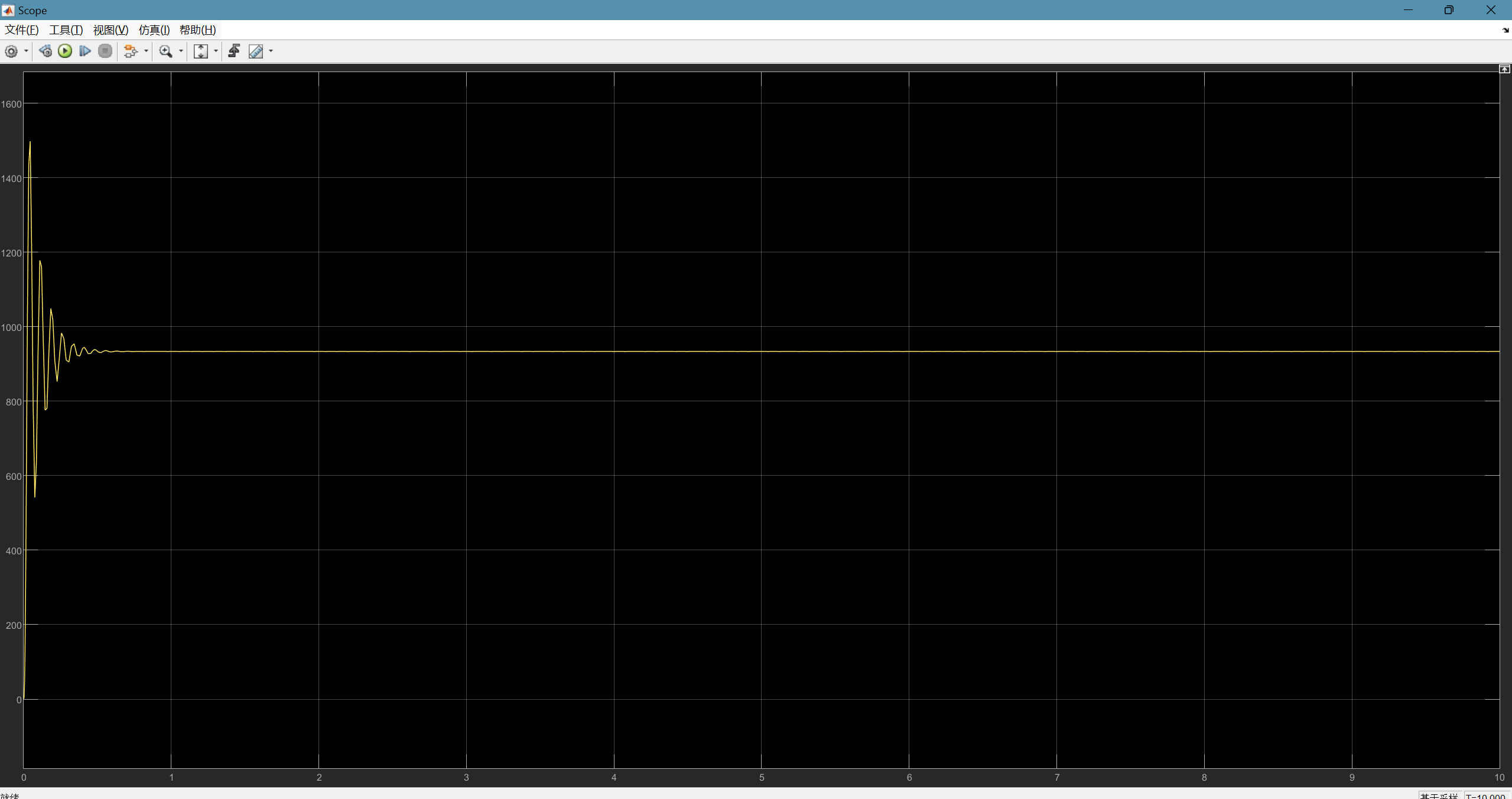

将系统输出连接至To WorkSpace模块上计算输出值

% 运行仿真后，在 MATLAB 中分析数据

simOut = sim('test'); % 替换为你的模型名称

outputData = simOut.get('outputData');

% 计算稳态值

steadyStateValue = mean(outputData(end-100:end)); % 取最后100个数据点的平均值

fprintf('稳态输出值: %.2f\n', steadyStateValue);